class: center, middle, inverse, title-slide .title[ # Lab2: Programming for populations in R ] .subtitle[ ## Iterative statements and finding numerical solutions in R ] .author[ ### Christopher Moore ] --- --- class: inverse, center, bottom background-image: url(https://www.hongkiat.com/blog/wp-content/uploads/programming-jokes/joke-shampoo.jpg) background-size: center # Iterative statements in R --- background-image: url(https://d33v4339jhl8k0.cloudfront.net/docs/assets/534421c6e4b09045db8e8a4b/images/5346a718e4b0b2c45b46a36b/file-ofGnbryhhh.gif) background-size: center class: inverse, center, bottom # Iterative statements in R --- # `for()` loops in R: the basics An iterative statement (*that tells the computer to do all of the work for you*) -- **Pseudocode:** `for (`variable in vector`) {` &nbsp;&nbsp;&nbsp;&nbsp;operation `}` -- **Code**: ```r for (i in 1:4) { print(i) } ## [1] 1 ## [1] 2 ## [1] 3 ## [1] 4 ``` --- # `for()` loops in R: saving output The idea is that you give `for()` a vector, and it performs an operation over it (**note a `for()` loop isn't needed for this, but it has heuristic value to do it**) -- **Code**: ```r my.vec <- rep(x = 0, times = 4) #rep means repeat, and the arguments are "x" to repeat and number of "times" my.vec ## [1] 0 0 0 0 for (i in 1:4) { # this saves to element `i` the value `i + 10` my.vec[i] <- i + 10 } my.vec ## [1] 11 12 13 14 ``` --- # `for()` loops in R: successive operations For perform an action based on a pervious value, and there are two common ways of doing this: -- **Example 1, code**: ```r n.steps <- 4 my.vec <- rep(x = 0, times = n.steps) initial.val <- 20 my.vec[1] <- initial.val for (i in 1:(n.steps - 1)) { # this saves to element `i + 1` the value `i + 10` my.vec[i+1] <- my.vec[i]*2 } ``` -- ```r my.vec ## [1] 20 40 80 160 ``` --- # `for()` loops in R: successive operations For perform an action based on a pervious value, and there are two common ways of doing this: -- **Example 2, code**: ```r n.steps <- 4 my.vec <- rep(x = 0, times = n.steps) initial.val <- 20 my.vec[1] <- initial.val for (i in 2:n.steps) { # this saves to element `i` the value `(i - 1) + 10` my.vec[i] <- my.vec[i-1]*2 } ``` -- ```r my.vec ## [1] 20 40 80 160 ``` --- # `for()` loops in R: a note on preallocation 1. Open R (or RStudio) 2. Create two vectors 1. One with a length of 0 (i.e., `c()`) 2. One with a length of 1 million (yes, we are about to do 1M things—I love loops) 3. Write two `for()` loops (one for each vector) from 1 to 1 million and let's just save the value of i to its corresponding element in the vector (e.g., i = 1 is the first element, i = 2 is the second) 4. Run the code a few times -- 5. Now, increase the length of both vectors to 10 million, and run one at a time for a few times: how long are they taking? -- 6. Now, increase the length of both vectors to 100 million! Try to time how long it takes each to loop through each vector. -- ### Take-home message: always preallocate! --- # `for()` loops in R: a note on preallocation ```r size <- 1e7 d.start <- proc.time() abc <- c() for (i in 1:size) { abc[i] <- i } d.end <- proc.time() p.start <- proc.time() cba <- vector(mode = "numeric", length = size) for (i in 1:size) { cba[i] <- i } p.end <- proc.time() d.end - d.start ## user system elapsed ## 1.296 0.137 1.437 p.end - p.start ## user system elapsed ## 0.277 0.023 0.315 ``` --- class: inverse, center, middle <iframe width="560" height="315" src="https://www.youtube.com/embed/v-pbGAts_Fg" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> # Numerical solutions in R --- # Solving initial-value problems in discrete and continuous time - Download package `deSolve` if not installed - There are many ways to do this, but `intall.packages(pkgs = "deSolve")` downloads straight from the Comprehensive R Archive Network - You only need to do this (1) the first time you use it and (2) whenever you reinstall R - Import into your library using `library(package = "deSolve")` --- # `ode()`: your new best friend for the semseter - Use `?ode` to navigate to help - `ode()` takes the arguments - `y`: A vector with the initial densities of your population - `times`: A vector of the times over which you wish to solve your problem - `func` A function that takes 3 arguments—time, state variable values, and parameters—and returns a list of derivatives - `parms`: A vector of the parameter values - `method`: "iteration" for discrete time, or nothing, "lsoda" (default), or any other for continuous time --- # `ode()` arguments, pt. 1 - `y`: Variable name must match what's in the function you pass on to `func`. For a 1-variable equation, just enter one element, e.g., `c(N = 0.5)`. For a 2+-variable equation, enter *n* elements, e.g., `c(N1 = 0.5, N2= 0.1, R1 = 4)`. - `times`: Nothing complicated here, just the time sequence; e.g., `seq(from = 0, to = 10, by. = 0.1)` - `parms`: Paramter names must match what's in the function you pass on to `func`. E.g., `c(r = 0.1, K = 42, alpha = 31)` --- # `ode()` arguments, pt. 2 - `func` - There are several ways of writing a function to pass to `ode()`, but I think it'd be worth using `with(as.list(c()))` because this matches your parameters from `parms` with what is in the equation. In general, here's how you want to write it using a logistic equation: ```r lositic <- function(time, state, pars) { with(as.list(c(state, pars)), { dN <- r*N*(K - N)/K return(list(c(dN))) }) } ``` --- # Set up to run `ode()` ```r logistic <- function(time, state, pars) { with(as.list(c(state, pars)), { dN <- r*N*(K - N)/K return(list(c(dN))) }) } N0 <- c(N = 0.1) parm_vec <- c(r = 1.2, K = 10) time_seq <- seq(from = 0, to = 15, by = 0.1) log_ode <- ode(y = N0, times = time_seq, func = logistic, parms = parm_vec) ``` --- # Output from `ode()`, pt. 1 ```r str(log_ode) ## 'deSolve' num [1:151, 1:2] 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ... ## - attr(*, "dimnames")=List of 2 ## ..$ : NULL ## ..$ : chr [1:2] "time" "N" ## - attr(*, "istate")= int [1:21] 2 155 311 NA 2 2 0 36 21 NA ... ## - attr(*, "rstate")= num [1:5] 0.1 0.1 15 0 0 ## - attr(*, "lengthvar")= int 1 ## - attr(*, "type")= chr "lsoda" head(log_ode) ## time N ## [1,] 0.0 0.1000000 ## [2,] 0.1 0.1126074 ## [3,] 0.2 0.1267815 ## [4,] 0.3 0.1427155 ## [5,] 0.4 0.1606195 ## [6,] 0.5 0.1807277 ``` --- # Output from `ode()`, pt. 2 ```r plot(x = log_ode[,1], y = log_ode[,2], xlab = "Time", ylab = "Density", las = 1, type = "l") ``` 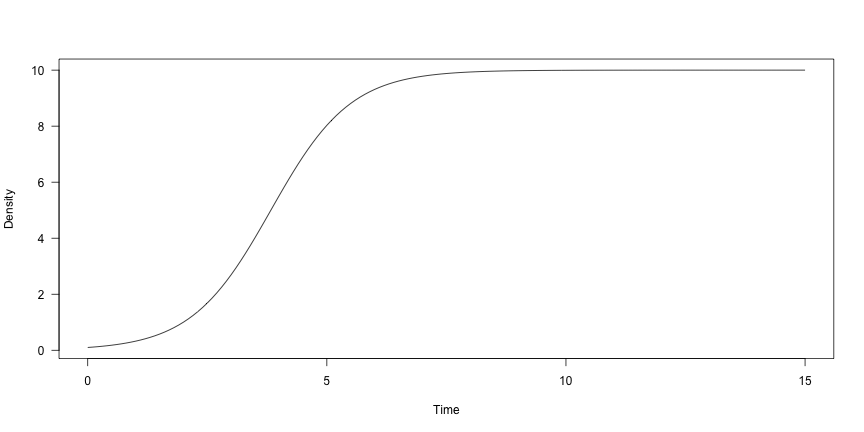<!-- -->